Search This Blog

Thursday, August 12, 2021

8/12/21 Report - Storms and What to Watch. Mudlarking or Sandsharking: Dolls.

Written by the Treasureguide for the exclusive use of the Treasure Beaches Report.


A few days ago I talked about mudlarking.  Mudlarking primarily involves searching the muddy tidal zone of rivers, such as the Thames, for old lost items.  It is said that the muddy banks of the Thames provides one of the richest archaeological sites in the world.  The finds there are certainly fascinating, and I know I'd love doing it.

In the past I've described what I called eye-balling.  That simply refers to searching for old lost items by sight rather than using a metal detector.  There is definitely a skill to it.

I sometimes search for bottles and things along the beaches and river banks, but where I search, there is no mud to speak of.  That is very important in a couple of ways.  First, sand and mud have an different consistency and behave differently.  Mud provides a nice protective layer that preserves objects. 

Since there is sand and almost no mud where I generally do my eye-balling, it seems the process should have a different name.  Right now I'm thinking of the term sandsharking.

One of the things I like most about mudlarking and sandsharking is the variety of types of finds.   There is much more to be found than just metal objects, though coins and other metal objects are also found.  Among the many things you can find are dolls and doll parts.  They tell of the children that lived and played in the area much more cheerfully, I would hope, than the original mudlarkers of London.

After lifting the doll's head (shown above) out of the sand and surrounding junk, I was immediately struck by the art of it even though it was broken.

That is something I like about sandsharking.  You often see nice lines, color and shapes, but there is also the story of those that were in the area in the past.  There is the history of the object and the feeling of its place in time and space.


This little ceramic doll (above) that came out of the sand and junk was undoubtedly a treasured toy of a child in the 1930s.  For me, it has a personal touch because my 95-year-old mother had one exactly like it.  In fact, I think I could probably if I looked for it.

On the back, it is incuse stamped MADE IN JAPAN - obviously prewar.  

It was found about 1200 miles from where my mother grew up, showing the similar culture shared by children of similar social class in distant areas of the country.

And not all sandsharked finds are worthless, even though very few are worth very much.


You might be surprised to learn that even doll parts can be worth money.  Above are a few that I've found.  Although I don't sell many finds other than bottles, I've probably sold about a half dozen arms and legs like the one shown on the bottom left of the above photo.  They are German made porcelain and are older than some of the others in the photo.  They always sell quickly.  I hope that they are used again, perhaps to repair or restore someone's damaged doll.

Here is the web site of a doll repair and restoration service.

Antique Doll Repair (luelstudio.com)

---

There is now some activity in the Atlantic.  There is tropical depression Fred.  It looks like Fred will be staying west of us, and producing tropical storm conditions in the Keys and West Florida.

Fred.
Source: nhc.noaa.gov.

We might get a three or four foot surf by Saturday - mostly from the southeast.

The next low pressure area following Fred could affect us.


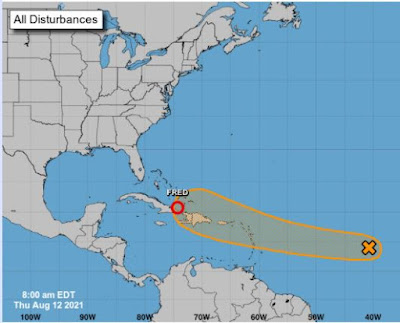Source: nhc. noaa.gov.

That one might remain a little more to the east.  We'll have to keep watching it.  It could come our way.

I'm not eager to see any major storms, but I sure would like to see some good beach erosion.

Good time to make sure your equipment is in good repair and ready.

Happy hunting,
Treasureguide@comcast.net











Today I will highlight some comments made in the Ogden document and elaborate on some of those.   First an excerpt from the Ogden document and then my comment.

Assessing the age and authenticity of antique or historic precious metal articles involves much more than just comparing their overall form and design with known parallels. It is also vital to look at the construction and constituents of jewellery. 

This is something I've discussed a lot in this blog.  It is one point I was making when I recently discussed floral rings.  It applies to other types of rings as well.  The similarity between a couple items does not mean they come from the same period, and it does not mean that either one is authentic.  You would expect copies to be similar, and you would expect fakes to look something like authentic examples, so the best fakes will not provide clues that are tremendously obvious.   Of course there are good and poor fakes.  As for design elements, there many that are so basic to the human experience and psyche that they will be found across broad ranges of time and cultures.  

Continuing with Ogden...

,,, few art historians, jewellers, jewellery collectors or auctioneers seem to be aware of the various ways in which technical criteria can be used to aid the dating and authentication of antique precious metal jewellery." ... As methods of analysis advance and become more accessible, it seems likely that the analysis of trace elements will become more and more common as a means of supporting opinions as to origin and authenticity. At the other end of the scale, even basic magnification equipment such as an inexpensive microscope or even 10x hand lens can reveal much with regards to technique and construction...

At present, advanced methods of analysis include things like XRF analysis which can provide more detailed technical data than is commonly available to the amateur population. 

I've found simple magnification very interesting and somewhat helpful. 

A few centuries ago jewelry would have been made using basic tools such as a rolling mill, piercing saw, die stamps, and hammer and would include techniques such as wire drawing, casting, and coloring.  Learning to find and recognize the signs left by the use of those tools is what the Ogden document is about, and that will help you identify the age and authenticity of jewelry items.

This demonstration video will also help you better understand the process and the use of those tools.


Here is the link to the Ogden pdf.




positive positive


false positive

negative negative

false  negative


I want to consider the large number of factors that should be considered when deciding if you should use discrimination.

Before getting started with that, there are four possible outcomes.   They are (1) correctly identifying a good signal and digging it, (2)  correctly identifying the lack of a good target, (


Here is a YouTube video showing how silver is turned into jewelry using a torch, hammer, rolling mill, and processes very much like those that would have been used centuries ago.  





===  



It is a noisy world.  There is always noise coming from the environment and there is always some level of internal noise, and noise creates uncertainty - sometimes more and sometimes less.

When metal detecting there are a variety of sources of external noise.  There can be electrical interference coming from electrical lines, cables, radio waves, lightning, and there can be noise coming from black sand, salt mineralization, loud noises from traffic or conversation..  Those are just a few examples.

There is also some level of internal noise too.  It can come from our brain or sensory system.  Did you ever think you heard someone call your name, but no one was there?   

We never have perfect concentration and our mind is always busy.   Our sensory system also generates noise.  We might have tinnitus, which makes it difficult to hear signals in a certain frequency range.  That is a very clear and concrete example.  

In metal detecting, the metal detector is engineered and the settings can be selected in an attempt to minimize external noise, while the detectorist will attempt to minimize internal by concentrating but there will always be some due to the natural operation of the nervous system.


Probability of Occurrence Curves

Figure 1 shows a graph of two hypothetical internal response curves. The curve on the left is for the noise-alone (healthy lung) trials, and the curve on the right is for the signal-plus-noise (tumor present) trials. The horizontal axis is labeled internal response and the vertical axis is labeled probability. The height of each curve represents how often that level of internal response will occur. For example, on noise-alone trials, there will generally be about 10 units of internal response: very little. However, there will be some trials with more (or less) internal response because of the internal noise.

Notice that we never lose the noise. The internal response for the signal-plus-noise case is generally greater but there is still a distribution (a spread) of possible responses. Notice also that the curves overlap, that is, the internal response for a noise-alone trial may exceed the internal response for a signal-plus-noise trial.

Figure 1: Internal response probability of occurrence curves for noise-alone and for signal-plus-noise trials.

Just to be really concrete, we could mark the horizontal axis in units of firing rate (10, 20, 30,..., etc. spikes per second). This would mean that on a noise-alone (no tumor) trial, it is most likely that the internal response would be 10 spikes per second. It is also rather likely that the internal response would be 5 or 15 spikes per second. But it is very unlikely that the internal response would be 25 spikes per second when no tumor is present. Because I want to remain noncommittal about what and where in the brain the internal response is, I did not label the horizontal axis in terms of firing rates. The internal response is in some unknown, but quantifiable, units.

The role of the criterion: Perhaps the simplest strategy that the doctor can adopt is to pick a criterion location along the internal response axis. Whenever the internal response is greater than this criterion, they respond "yes". Whenever the internal response is less than this criterion, they respond "no".

An example criterion is indicated by the vertical lines in Figure 2. The criterion line divides the graph into four sections that correspond to hits, misses, false alarms, and correct rejections. On both hits and false alarms, the internal response is greater than the criterion, because the doctor is responding "yes''. Hits correspond to signal-plus-noise trials when the internal response is greater than criterion, as indicated in the upper figure. False alarms correspond to noise-alone trials when the internal response is greater than criterion, as indicated in the lower figure.

Figure 2: Internal response probability of occurrence curves for noise-alone and signal-plus-noise trials. Since the curves overlap, the internal response for a noise-alone trial may exceed the internal response for a signal-plus-noise trial. Vertical lines correspond to the criterion response.

Suppose that the doctor chooses a low criterion (Figure 3, top), so that they respond "yes'' to almost everything. Then they will never miss a tumor when it is present and they will therefore have a very high hit rate. On the other hand, saying "yes'' to almost everything will greatly increase the number of false alarms (potentially leading to unnecessary surgeries). Thus, there is a clear cost to increasing the number of hits, and that cost is paid in terms of false alarms. If the doctor chooses a high criterion (Figure 3, bottom) then they respond "no'' to almost everything. They will rarely make a false alarm, but they will also miss many real tumors.

Figure 3: Effect of shifting the criterion

Notice that there is no way that the doctor can set their criterion to achieve only hits and no false alarms. The message that you should be taking home from this is that it is inevitable that some mistakes will be made. Because of the noise it is simply a true, undeniable fact that the internal responses on noise-alone trials may exceed the internal responses on signal-plus-noise trials in some instances. Thus, a doctor cannot always be right. They can adjust the kind of errors that they make by manipulating their criterion, the one part of this diagram that is under their control.

The Receiver Operating Characteristic

We can describe the full range of the doctor's options in a single curve, called an ROC curve, which stands for receiver operating characteristic. The ROC curve captures, in a single graph, the various alternatives that are available to the doctor as they move their criterion to higher and lower levels.

ROC curves (Figure 4) are plotted with the false alarm rate on the horizontal axis and the hit rate on the vertical axis. The figure shows several different ROC curves, each corresponding to a different signal strength. Just pay attention to one of them (the curve labeled d'=1) for the time being. We already know that if the criterion is very high, then both the false alarm rate and the hit rate will be very low, putting you somewhere near the lower left corner of the ROC graph. If   the criterion is very low, then both the hit rate and the false alarm rate will be very high, putting you somewhere near the upper right corner of the graph.  For an intermediate choice of criterion, the hit rate and false alarm rate will take on intermediate values. The ROC curve characterizes the choices available to the doctor. They may set the criterion anywhere, but any choice that they make will land them with a hit and false alarm rate somewhere on the ROC curve. Notice also that for any reasonable choice of criterion, the hit rate is always larger than the false alarm rate, so the ROC curve is bowed upward.





















at